Berechnungsaufgabe

Schritt für Schritt

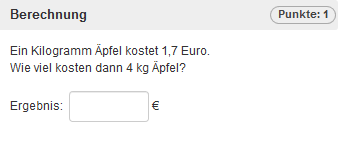
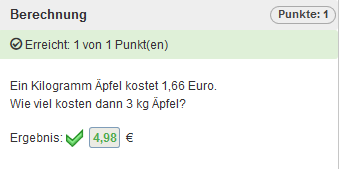
Im Folgenden wird die Erstellung einer Berechnungsaufgabe, anhand der abgebildeten Beispielaufgabe erklärt.

Schritt 1: Konzeption der Aufgabe

Als Beispiel soll eine Berechnungsaufgabe mit einer gegebenen Funktion erstellt werden. Der Lernende soll die Fläche unter dieser Funktion in einem gegebenen Intervall berechnen. Als Parameter dienen die Faktoren der Funktionsgleichung und die Intervallgrenzen. Alle Parameter sollen als zufällige, ganzzahlige Werte in einem gegebenen Intervall ermittelt werden.

Schritt 2: Definition der Parameter

Wechseln Sie in das Tab „Variablen“ und erstellen Sie vier neue Variablen. Vergeben Sie als Variablen-Name entsprechend dem Konzept die Identifier „a“, „b“, „c“ und „d“. Alle Variablen sind vom Typ „Ganze Zahl“. Zur Wertermittlung nutzen wir die Funktion „Zufällige Auswahl“ und definieren einen Wertebereich.

Für den Einsatz von Konstanten verwenden Sie auch "Zufällige Auswahl" und geben anschließend nur den einzelnen Wert für die zu verwendende Konstante vor.

Eine detaillierte Beschreibung zum Anlegen und Einfügen von Variablen erhalten Sie in der Hilfe-Beschreibung zur Verwendung von Variablen.

Abb: Variable definieren

Schritt 3: Erstellung der Aufgabenstellung

Wechseln Sie in das Tab „Frage & Antwort“ und geben Sie die Fragestellung in das Textfeld ein. Formeln können Sie mit LaTeX direkt in den Aufgabentext integrieren (Hilfe zur Formeleingabe). Um die definierten Variablen als Parameter in der Funktion zu nutzen, geben Sie einfach an die entsprechende Stelle den Variablennamen in geschweiften Klammern ein (bspw. {a}). ONYX erkennt automatisch, dass es sich um eine definierte Variable handelt und ersetzt diese entsprechend bei der Testdurchführung. Die Angabe von Variablennamen ist innerhalb von LaTeX, als auch im normalen Text möglich.

Abb: Erstellung Aufgabenstellung

Schritt 4: Erstellung der Berechnungsvorschrift

Klicken Sie mit der Maus auf das Lückensymbol  oder erstellen Sie eine neue Lücke mit Hilfe des Buttons „Lücke hinzufügen“. Es öffnet sich das Bearbeiten-Fenster für die gewählte Lücke. Wählen Sie nun die Option „Neue Variable definieren“. Sie gelangen automatisch zum Tab Variablen und es wurde eine neue Variable mit dem Identifier „solution“, vom Typ „Ganze Zahl“ (oder „Gleitkommazahl“) erstellt. Zur Wert-Ermittlung ist bereits die Option „Berechnung“ ausgewählt. Da wir als Lösung eine „Gleitkommazahl“ erwarten, wechseln wir den Typ nach „Gleitkommazahl“. Geben Sie nun die Berechnungsvorschrift in das vorgesehene Eingabefeld ein. Verwenden Sie auch hier die Parameter durch Angabe des Variablennamens in geschweiften Klammern (bspw. {a}). Die Berechnungsvorschrift wird in MAXIMA-Schreibweise angegeben.

Im Tab „Frage und Antwort“ wurde als Lösung automatisch die neue Variable „solution“ ausgewählt.

Abb: Berechnungsvorschrift

Schritt 5 (optional): Definition eines Toleranzbereiches

Um bei „Gleitkommazahlen“ unabhängig von der Genauigkeit des Ergebniswertes, eine beispielsweise auf zwei Dezimalstellen genau Lösung abzufragen, definieren wir eine absolute Abweichung von „0,01“, ohne Einbeziehung der Toleranzgrenzen.

Eine detaillierte Beschreibung zur Option „Genauigkeit“ erhalten Sie in der Hilfe-Beschreibung zur Numerischen Eingabe.

Abb: Toleranzbereichen festlegen

Schritt 6: Überprüfung der Aufgabe

Wählen Sie nun die Option „Vorschau“, um eine zufällig generierte Beispielaufgabe Ihrer Berechnungsvorschrift anzuzeigen. Bei jedem Aufruf der Vorschau wird die Aufgabe neu generiert. Die Vorschau bietet Ihnen auch die Möglichkeit zur Überprüfung der Lösungseingabe.

Abb: Überprüfung der Aufgabe

Beispiel Gleitkommazahlen

Ziel: In einer Aufgabe soll eine ganze Zahl mit einer Gleitkommazahl multipliziert werden.

Anlegen eine Berechnungsaufgabe und Definition von Variablen:

Formulierung der Fragestellung zur Multiplikation der angezeigten Werte:

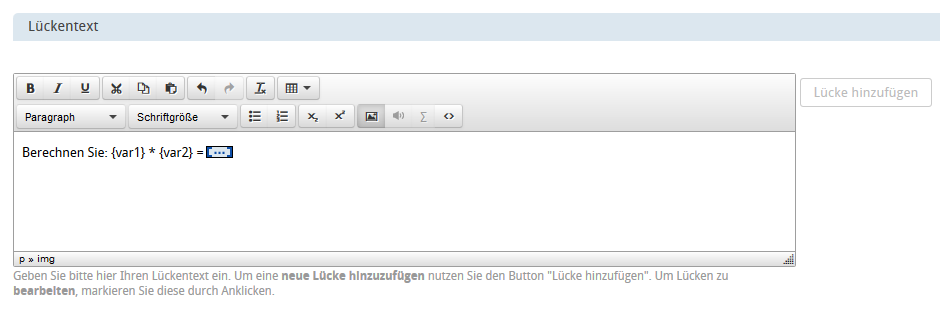
Die Auswertung der Nutzereingabe erfolgt in der Standarteinstellung mit "exakter" Genauigkeit:

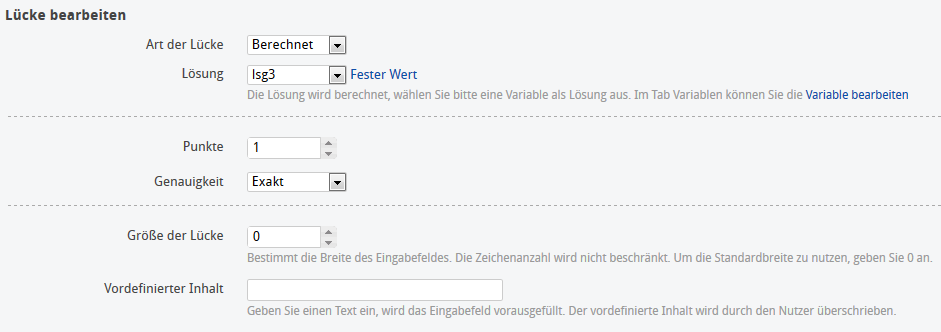
Der Nutzer kann keine richtige Lösung eingeben. Die Variable mit der Gleitkommazahl wird in diesem Fall mit 4 Nachkommastellen angezeigt. Die exakte Berechnung erfolgt jedoch mit dem exakten Zufallswert der Variable.

Lösung: Mit der Einstellung "Genauigkeit: Absolut" wird ein Toleranzbereich für die Berechnung der Lücke definiert.

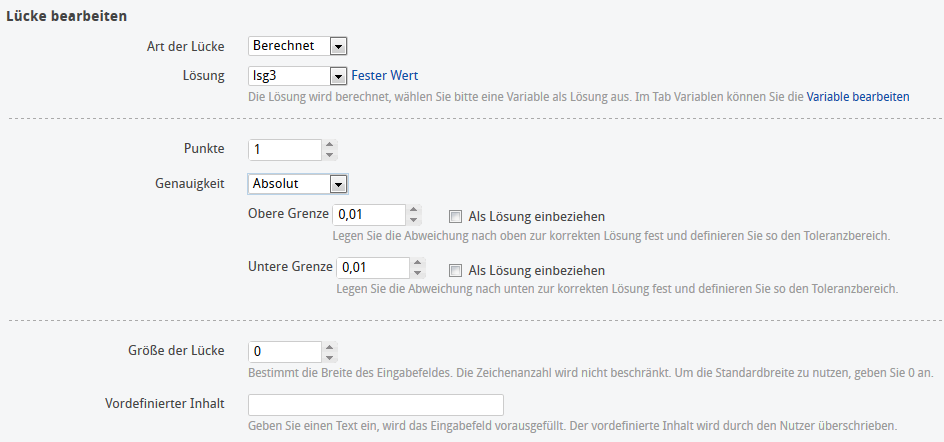
Mit der Wahl eines geeigneten Intervalls wird das Ergebnis richtig bewertet.

Step by step

In the following, the creation of a calculation interaction is explained by means of an example.

Step 1: Design the task

As an example, a calculation interaction is to be created with a given function. The task of the learner is to calculate the area under this function at a given interval. The factors of the function equation and the interval boundaries serve as parameters. All parameters are supposed to be determined as random, integer values in a given interval.

Step 2: Parameter definition

Switch to the tab "Variables" and create four new variables. Assign the identifiers "a", "b", "c", and "d" as variable names. All variables are of the type "integer". To determine values for the variables, use the function "Random" and define a value range.

In the case of constants, use "Random" and enter only the individual value for the constant.

A detailed description of how to create and insert variables can be found in the help section Using variables.

Fig.: Define variable

Step 4: Creation of the calculation rule

Click on the gap symbol  or create a new gap via the button "Add gap". The edit window for the selected gap opens. Select the option "Define new variable". You will then be automatically directed to the tab "Variables", and a new variable with the identifier "solution" of the type "integer" (or "floating-point") will be created. For the value determination, the option "Calculation" is already selected.

Since we expect a floating-point number as a solution, the variable type should be changed to "floating-point". Enter then the calculation rule in the appropriate input field below. Parameters are used by specifying the variable name in braces (e.g. {a}). The calculation rule is specified in MAXIMA notation.

In the tab "Question and Answer", the new variable "solution" was automatically selected as the solution.

Fig.: Calculation rule

Step 5 (optional): Definition of a tolerance range

To retrieve a solution that is, for example, accurate to two decimal places regardless of the accuracy of the result value, we define an absolute deviation of "0.01", without including the tolerance limits.

A more detailed description on the option "Precision" is provided in the help section Numerical input interaction.

Fig.: Set tolerance range

Step 6: Task verification

Select the option "Preview" to display a randomly generated example task of your calculation rule. The task is regenerated each time you preview it. The preview also provides you with the possibility to check the solution input.

Fig.: Task verification

Example floating-point numbers

Goal: In a task, an integer is to be multiplied by a floating-point number.

Creating a calculation interaction and defining variables:

Formulation of the question concerning the multiplication of the displayed values:

The user input is by default evaluated with "exact" precision:

The user cannot enter a correct solution. The variable with the floating-point number is displayed with 4 decimal places in this case. The exact calculation, however, is performed with the exact random value of the variable.

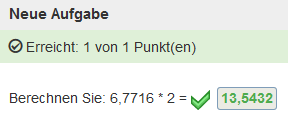
Solution: Via the setting "Precision: Absolute", a tolerance range can be defined for the calculation of the gap.

By selecting a suitable interval, the result will be properly assessed.